What Is the Electric Flux Through the Circle When Its Face Is Perpendicular to the Field Lines?
Gauss's Constabulary
37 Electrical Flux
Learning Objectives
Past the stop of this department, y'all will be able to:
- Define the concept of flux
- Describe electric flux
- Summate electric flux for a given situation
The concept of flux describes how much of something goes through a given area. More formally, it is the dot production of a vector field (in this affiliate, the electrical field) with an area. You may conceptualize the flux of an electrical field every bit a measure of the number of electric field lines passing through an area ((Figure)). The larger the expanse, the more field lines become through it and, hence, the greater the flux; similarly, the stronger the electrical field is (represented past a greater density of lines), the greater the flux. On the other hand, if the area rotated and so that the plane is aligned with the field lines, none will laissez passer through and there will exist no flux.
The flux of an electric field through the shaded area captures data nearly the "number" of electric field lines passing through the area. The numerical value of the electric flux depends on the magnitudes of the electrical field and the area, as well as the relative orientation of the surface area with respect to the direction of the electric field.
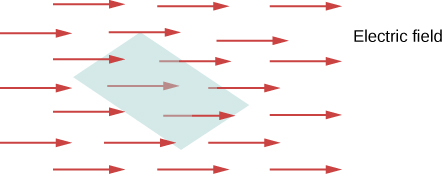
A macroscopic analogy that might assist you imagine this is to put a hula hoop in a flowing river. Equally y'all change the angle of the hoop relative to the management of the electric current, more or less of the menstruation will go through the hoop. Similarly, the amount of menstruum through the hoop depends on the force of the current and the size of the hoop. Again, flux is a general concept; we can also use it to draw the amount of sunlight hit a solar console or the amount of energy a telescope receives from a afar star, for example.
To quantify this idea, (Figure)(a) shows a planar surface ![]() of area
of area ![]() that is perpendicular to the uniform electric field
that is perpendicular to the uniform electric field ![]() If N field lines laissez passer through
If N field lines laissez passer through ![]() , then we know from the definition of electric field lines (Electric Charges and Fields) that
, then we know from the definition of electric field lines (Electric Charges and Fields) that ![]() or
or ![]()
The quantity ![]() is the electrical flux through
is the electrical flux through ![]() . We represent the electric flux through an open surface like
. We represent the electric flux through an open surface like ![]() by the symbol
by the symbol ![]() . Electric flux is a scalar quantity and has an SI unit of newton-meters squared per coulomb (
. Electric flux is a scalar quantity and has an SI unit of newton-meters squared per coulomb (![]() ). Notice that
). Notice that ![]() may also be written equally
may also be written equally ![]() , demonstrating that electric flux is a measure of the number of field lines crossing a surface.
, demonstrating that electric flux is a measure of the number of field lines crossing a surface.
Now consider a planar surface that is non perpendicular to the field. How would we represent the electric flux? (Figure)(b) shows a surface ![]() of surface area
of surface area ![]() that is inclined at an bending
that is inclined at an bending ![]() to the xz-plane and whose projection in that plane is
to the xz-plane and whose projection in that plane is ![]() (surface area
(surface area ![]() ). The areas are related by
). The areas are related by ![]() Because the same number of field lines crosses both
Because the same number of field lines crosses both ![]() and
and ![]() , the fluxes through both surfaces must exist the same. The flux through
, the fluxes through both surfaces must exist the same. The flux through ![]() is therefore
is therefore ![]() Designating
Designating ![]() equally a unit vector normal to
equally a unit vector normal to ![]() (see (Figure)(b)), nosotros obtain
(see (Figure)(b)), nosotros obtain
![]()
Bank check out this video to observe what happens to the flux as the area changes in size and angle, or the electrical field changes in strength.
Area Vector
For discussing the flux of a vector field, it is helpful to innovate an area vector ![]() This allows us to write the last equation in a more compact grade. What should the magnitude of the area vector be? What should the management of the area vector be? What are the implications of how you answer the previous question?
This allows us to write the last equation in a more compact grade. What should the magnitude of the area vector be? What should the management of the area vector be? What are the implications of how you answer the previous question?
The area vector of a flat surface of expanse A has the post-obit magnitude and management:
- Magnitude is equal to area (A)
- Direction is along the normal to the surface (
 ); that is, perpendicular to the surface.
); that is, perpendicular to the surface.
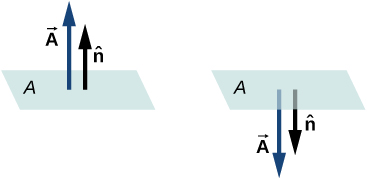
Since the normal to a apartment surface can point in either direction from the surface, the direction of the expanse vector of an open surface needs to be called, as shown in (Figure).
The management of the expanse vector of an open surface needs to be chosen; information technology could be either of the two cases displayed here. The area vector of a part of a closed surface is defined to bespeak from the inside of the closed space to the outside. This rule gives a unique management.
Since ![]() is a unit of measurement normal to a surface, it has 2 possible directions at every point on that surface ((Effigy)(a)). For an open surface, we can use either direction, as long as we are consequent over the entire surface. Function (c) of the figure shows several cases.
is a unit of measurement normal to a surface, it has 2 possible directions at every point on that surface ((Effigy)(a)). For an open surface, we can use either direction, as long as we are consequent over the entire surface. Function (c) of the figure shows several cases.
(a) Two potential normal vectors arise at every point on a surface. (b) The outward normal is used to summate the flux through a closed surface. (c) Only ![]() has been given a consistent ready of normal vectors that allows us to define the flux through the surface.
has been given a consistent ready of normal vectors that allows us to define the flux through the surface.
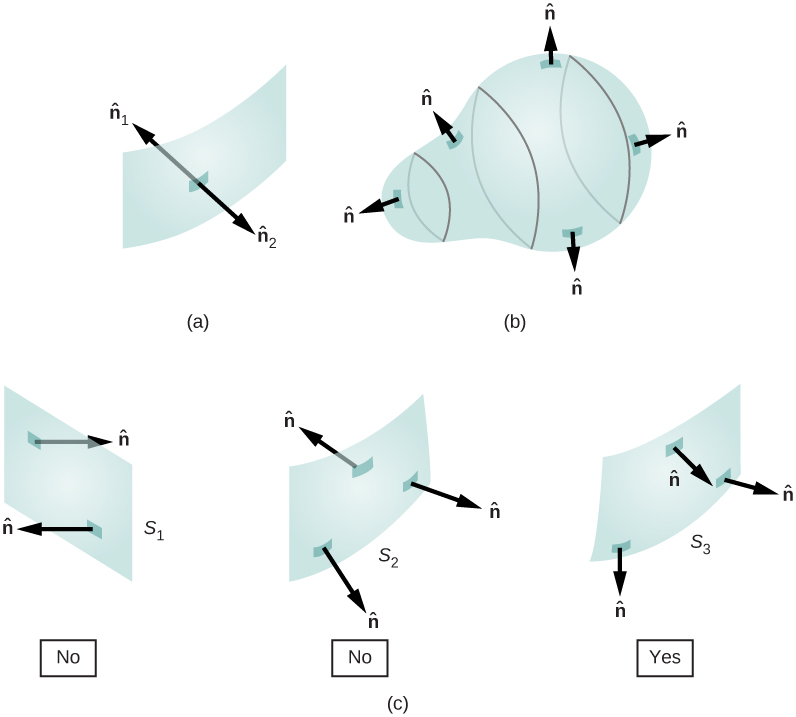
However, if a surface is closed, then the surface encloses a volume. In that instance, the direction of the normal vector at whatsoever point on the surface points from the inside to the exterior. On a closed surface such as that of (Effigy)(b), ![]() is chosen to be the outward normal at every indicate, to exist consistent with the sign convention for electric accuse.
is chosen to be the outward normal at every indicate, to exist consistent with the sign convention for electric accuse.
Electric Flux
Now that we have defined the area vector of a surface, we can ascertain the electric flux of a compatible electric field through a apartment area as the scalar product of the electrical field and the area vector, as defined in Products of Vectors:
![]()
(Figure) shows the electric field of an oppositely charged, parallel-plate system and an imaginary box betwixt the plates. The electrical field between the plates is uniform and points from the positive plate toward the negative plate. A calculation of the flux of this field through various faces of the box shows that the net flux through the box is zero. Why does the flux cancel out here?
Electric flux through a cube, placed betwixt two charged plates. Electrical flux through the lesser face (ABCD) is negative, because ![]() is in the contrary direction to the normal to the surface. The electric flux through the top face (FGHK) is positive, because the electric field and the normal are in the same direction. The electric flux through the other faces is cipher, since the electric field is perpendicular to the normal vectors of those faces. The net electric flux through the cube is the sum of fluxes through the six faces. Here, the cyberspace flux through the cube is equal to zero. The magnitude of the flux through rectangle BCKF is equal to the magnitudes of the flux through both the peak and bottom faces.
is in the contrary direction to the normal to the surface. The electric flux through the top face (FGHK) is positive, because the electric field and the normal are in the same direction. The electric flux through the other faces is cipher, since the electric field is perpendicular to the normal vectors of those faces. The net electric flux through the cube is the sum of fluxes through the six faces. Here, the cyberspace flux through the cube is equal to zero. The magnitude of the flux through rectangle BCKF is equal to the magnitudes of the flux through both the peak and bottom faces.
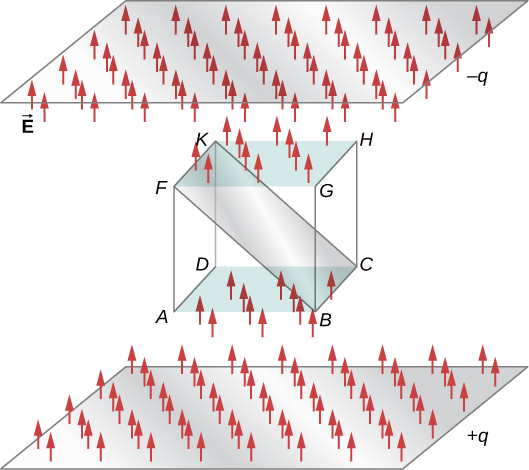
The reason is that the sources of the electric field are exterior the box. Therefore, if whatever electric field line enters the volume of the box, it must also exit somewhere on the surface because at that place is no charge inside for the lines to land on. Therefore, quite generally, electric flux through a closed surface is nix if in that location are no sources of electric field, whether positive or negative charges, inside the enclosed volume. In general, when field lines leave (or "period out of") a closed surface, ![]() is positive; when they enter (or "menses into") the surface,
is positive; when they enter (or "menses into") the surface, ![]() is negative.
is negative.
Any shine, not-flat surface can be replaced past a drove of tiny, approximately apartment surfaces, as shown in (Effigy). If we divide a surface Due south into small patches, so we notice that, as the patches become smaller, they tin can be approximated by flat surfaces. This is similar to the mode nosotros treat the surface of Earth as locally flat, even though we know that globally, it is approximately spherical.
A surface is divided into patches to discover the flux.
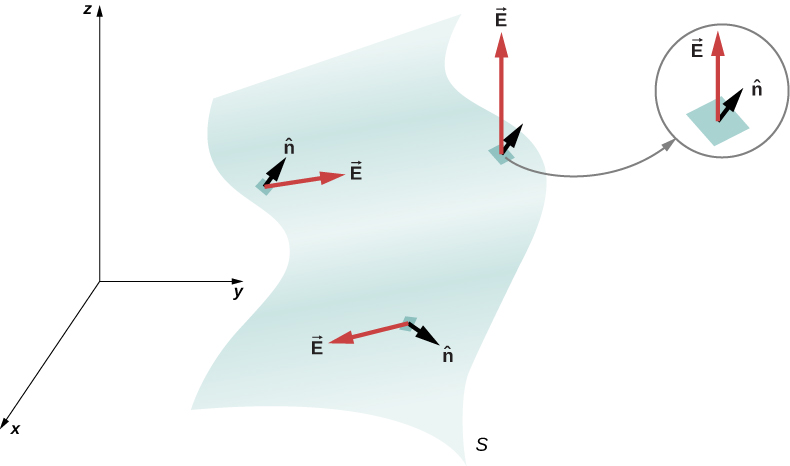
To keep track of the patches, nosotros can number them from i through N . At present, we define the surface area vector for each patch every bit the area of the patch pointed in the direction of the normal. Let us denote the expanse vector for the ith patch past ![]() (We have used the symbol
(We have used the symbol ![]() to remind united states of america that the area is of an arbitrarily small patch.) With sufficiently small patches, we may approximate the electric field over any given patch equally uniform. Permit united states announce the average electric field at the location of the ith patch by
to remind united states of america that the area is of an arbitrarily small patch.) With sufficiently small patches, we may approximate the electric field over any given patch equally uniform. Permit united states announce the average electric field at the location of the ith patch by ![]()
![]()
Therefore, we tin write the electric flux ![]() through the area of the ith patch every bit
through the area of the ith patch every bit
![]()
The flux through each of the private patches can be constructed in this manner and then added to give u.s. an guess of the cyberspace flux through the unabridged surface S, which nosotros denote just as ![]() .
.
![]()
This estimate of the flux gets better as we decrease the size of the patches. Withal, when you utilize smaller patches, y'all need more than of them to embrace the same surface. In the limit of infinitesimally small patches, they may be considered to have surface area dA and unit normal ![]() . Since the elements are infinitesimal, they may be assumed to exist planar, and
. Since the elements are infinitesimal, they may be assumed to exist planar, and ![]() may be taken as constant over whatsoever element. Then the flux
may be taken as constant over whatsoever element. Then the flux ![]() through an area dA is given by
through an area dA is given by ![]() It is positive when the angle between
It is positive when the angle between ![]() and
and ![]() is less than
is less than ![]() and negative when the bending is greater than
and negative when the bending is greater than ![]() . The net flux is the sum of the infinitesimal flux elements over the entire surface. With infinitesimally small patches, you need infinitely many patches, and the limit of the sum becomes a surface integral. With
. The net flux is the sum of the infinitesimal flux elements over the entire surface. With infinitesimally small patches, you need infinitely many patches, and the limit of the sum becomes a surface integral. With ![]() representing the integral over S,
representing the integral over S,
![]()
In practical terms, surface integrals are computed by taking the antiderivatives of both dimensions defining the area, with the edges of the surface in question being the bounds of the integral.
To distinguish between the flux through an open up surface similar that of (Effigy) and the flux through a closed surface (ane that completely premises some book), we represent flux through a closed surface by
![]()
where the circumvolve through the integral symbol merely means that the surface is closed, and nosotros are integrating over the entire matter. If you lot only integrate over a portion of a airtight surface, that means yous are treating a subset of it as an open surface.
Flux of a Uniform Electric Field A abiding electric field of magnitude ![]() points in the direction of the positive z-axis ((Effigy)). What is the electric flux through a rectangle with sides a and b in the (a) xy-plane and in the (b) xz-plane?
points in the direction of the positive z-axis ((Effigy)). What is the electric flux through a rectangle with sides a and b in the (a) xy-plane and in the (b) xz-plane?
Calculating the flux of ![]() through a rectangular surface.
through a rectangular surface.
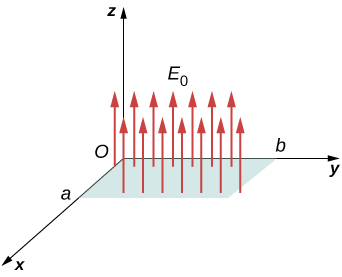
Strategy Apply the definition of flux: ![]() , where the definition of dot production is crucial.
, where the definition of dot production is crucial.
Solution
- In this case,
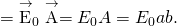
- Here, the direction of the surface area vector is either along the positive y-axis or toward the negative y-axis. Therefore, the scalar production of the electric field with the surface area vector is zero, giving zero flux.
Significance The relative directions of the electric field and area can cause the flux through the surface area to be nil.
Flux of a Compatible Electric Field through a Airtight Surface A constant electrical field of magnitude ![]() points in the direction of the positive z-axis ((Effigy)). What is the net electric flux through a cube?
points in the direction of the positive z-axis ((Effigy)). What is the net electric flux through a cube?
Computing the flux of ![]() through a closed cubic surface.
through a closed cubic surface.

Strategy Apply the definition of flux: ![]() , noting that a closed surface eliminates the ambiguity in the direction of the area vector.
, noting that a closed surface eliminates the ambiguity in the direction of the area vector.
Solution Through the acme face of the cube, ![]()
Through the bottom face of the cube, ![]() because the area vector here points down.
because the area vector here points down.
Along the other four sides, the direction of the expanse vector is perpendicular to the direction of the electric field. Therefore, the scalar production of the electric field with the area vector is zippo, giving zero flux.
The internet flux is ![]() .
.
Significance The net flux of a uniform electrical field through a airtight surface is zero.
Electric Flux through a Plane, Integral Method A compatible electric field ![]() of magnitude x N/C is directed parallel to the yz-aeroplane at
of magnitude x N/C is directed parallel to the yz-aeroplane at ![]() above the xy-plane, as shown in (Figure). What is the electrical flux through the plane surface of area
above the xy-plane, as shown in (Figure). What is the electrical flux through the plane surface of area ![]() located in the xz-plane? Assume that
located in the xz-plane? Assume that ![]() points in the positive y-direction.
points in the positive y-direction.
The electric field produces a net electric flux through the surface Due south.
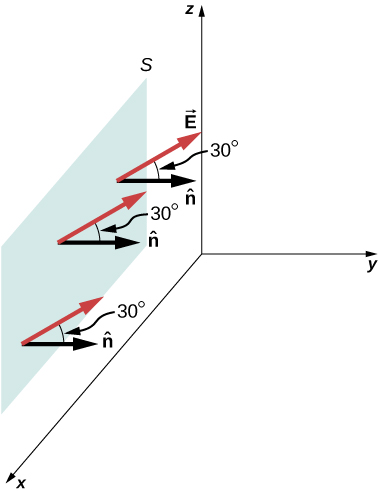
Strategy Apply ![]() , where the direction and magnitude of the electric field are abiding.
, where the direction and magnitude of the electric field are abiding.
Solution The bending between the uniform electrical field ![]() and the unit normal
and the unit normal ![]() to the planar surface is
to the planar surface is ![]() . Since both the direction and magnitude are abiding, Eastward comes outside the integral. All that is left is a surface integral over dA, which is A. Therefore, using the open up-surface equation, nosotros find that the electrical flux through the surface is
. Since both the direction and magnitude are abiding, Eastward comes outside the integral. All that is left is a surface integral over dA, which is A. Therefore, using the open up-surface equation, nosotros find that the electrical flux through the surface is

Significance Again, the relative directions of the field and the area matter, and the general equation with the integral volition simplify to the elementary dot product of surface area and electric field.
Check Your Understanding What angle should in that location be between the electrical field and the surface shown in (Effigy) in the previous instance and so that no electric flux passes through the surface?
Place it then that its unit normal is perpendicular to ![]()
Inhomogeneous Electric Field What is the total flux of the electric field ![]() through the rectangular surface shown in (Figure)?
through the rectangular surface shown in (Figure)?
Since the electrical field is not abiding over the surface, an integration is necessary to make up one's mind the flux.
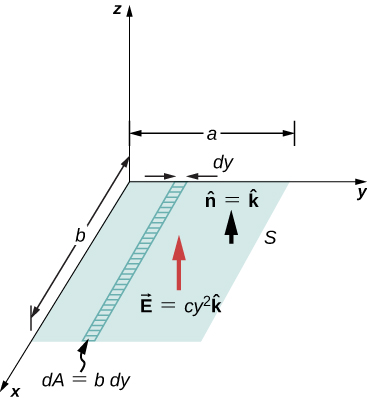
Strategy Apply ![]() . We assume that the unit normal
. We assume that the unit normal ![]() to the given surface points in the positive z-direction, so
to the given surface points in the positive z-direction, so ![]() Since the electric field is non uniform over the surface, it is necessary to divide the surface into infinitesimal strips forth which
Since the electric field is non uniform over the surface, it is necessary to divide the surface into infinitesimal strips forth which ![]() is substantially abiding. As shown in (Effigy), these strips are parallel to the x-axis, and each strip has an expanse
is substantially abiding. As shown in (Effigy), these strips are parallel to the x-axis, and each strip has an expanse ![]()
Solution From the open surface integral, we discover that the net flux through the rectangular surface is
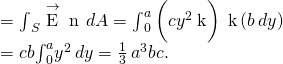
Significance For a non-constant electric field, the integral method is required.
Check Your Understanding If the electric field in (Effigy) is ![]() what is the flux through the rectangular area?
what is the flux through the rectangular area?
![]()
Summary
- The electric flux through a surface is proportional to the number of field lines crossing that surface. Note that this means the magnitude is proportional to the portion of the field perpendicular to the surface area.
- The electric flux is obtained past evaluating the surface integral
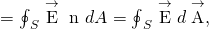
where the notation used here is for a closed surface South.
Conceptual Questions
Discuss how to orient a planar surface of area A in a uniform electrical field of magnitude ![]() to obtain (a) the maximum flux and (b) the minimum flux through the area.
to obtain (a) the maximum flux and (b) the minimum flux through the area.
a. If the planar surface is perpendicular to the electric field vector, the maximum flux would be obtained. b. If the planar surface were parallel to the electrical field vector, the minimum flux would be obtained.
What are the maximum and minimum values of the flux in the preceding question?
The cyberspace electric flux crossing a airtight surface is always nil. True or false?
Simulated. The net electrical flux crossing a airtight surface is e'er zero if and merely if the cyberspace accuse enclosed is zip.
The net electric flux crossing an open up surface is never naught. True or simulated?
Problems
A uniform electric field of magnitude ![]() is perpendicular to a foursquare sheet with sides 2.0 m long. What is the electrical flux through the sheet?
is perpendicular to a foursquare sheet with sides 2.0 m long. What is the electrical flux through the sheet?
Calculate the flux through the sheet of the previous problem if the plane of the canvas is at an angle of ![]() to the field. Notice the flux for both directions of the unit normal to the sheet.
to the field. Notice the flux for both directions of the unit normal to the sheet.
![]() electric field in direction of unit of measurement normal;
electric field in direction of unit of measurement normal; ![]() electric field reverse to unit normal
electric field reverse to unit normal
The electric flux through a square-shaped area of side 5 cm near a big charged sheet is plant to be ![]() when the expanse is parallel to the plate. Find the charge density on the sheet.
when the expanse is parallel to the plate. Find the charge density on the sheet.
![]()
Consider the uniform electric field ![]() What is its electric flux through a round surface area of radius 2.0 k that lies in the xy-plane?
What is its electric flux through a round surface area of radius 2.0 k that lies in the xy-plane?
![]()
Repeat the previous problem, given that the circular area is (a) in the yz-aeroplane and (b) ![]() above the xy-plane.
above the xy-plane.
An infinite charged wire with charge per unit of measurement length ![]() lies along the central axis of a cylindrical surface of radius r and length fifty. What is the flux through the surface due to the electrical field of the charged wire?
lies along the central axis of a cylindrical surface of radius r and length fifty. What is the flux through the surface due to the electrical field of the charged wire?
![]()
Glossary
- area vector
- vector with magnitude equal to the surface area of a surface and direction perpendicular to the surface
- electric flux
- dot production of the electric field and the area through which it is passing
- flux
- quantity of something passing through a given area
Source: https://opentextbc.ca/universityphysicsv2openstax/chapter/electric-flux/